2019-2020学年上海黄浦区大同初级中学初一(上)十月月考数学试题
1、选择题(本大题共6小题,共18.0分)
下列代数式中,符合书写需要的是
A. a3 B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【分析】解:A、数与字母的乘积,应把数字因数写在字母的前面,故A错误;
B、系数应化成假分数的形式,故B错误;
C、应写成分式的形式,故C错误;
D、单项式的系数是假分数,故D正确;
故选:D.
依据代数式的表达方法,可得答案.
本题考察了代数式,代数式的书写需要:![]() 在代数式中出现的乘号,一般简写成“
在代数式中出现的乘号,一般简写成“![]() ”或者省略不写;
”或者省略不写;![]() 数字与字母相乘时,数字要写在字母的前面;
数字与字母相乘时,数字要写在字母的前面;![]() 在代数式中出现的除法运算,一般根据分数的写法来写
在代数式中出现的除法运算,一般根据分数的写法来写![]() 带分数要写成假分数的形式.
带分数要写成假分数的形式.
某产品降价![]() 后,每台价格a元,那样该产品原价应为元.
后,每台价格a元,那样该产品原价应为元.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【分析】解:![]() 某产品降价
某产品降价![]() 后,每台价格a元,
后,每台价格a元,![]() 该产品原价应为:
该产品原价应为:![]()
故选:D.
直接借助价格除以![]() 原价,进而得出答案.
原价,进而得出答案.
此题主要考查了列代数式,正确理解原件与降价前关系是解题重点.
已知M是一个五次多项式,N是一个三次多项式,则![]() 肯定是
肯定是
A. 五次多项式 B. 五次整式 C. 多项式 D. 单项式
【答案】B
【分析】解:已知M是一个五次多项式,N是一个三次多项式,则![]() 肯定是五次整式,
肯定是五次整式,
故选:B.
借助合并相同种类项法则判断即可.
此题考查了整式的加减,熟练学会运算法则是解本题的重点.
下列运算中与![]() 结果相同的是
结果相同的是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【分析】解:A、原式![]() ,不合题意;
,不合题意;
B、原式![]() ,不合题意;
,不合题意;
C、原式![]() ,不合题意;
,不合题意;
D、原式![]() ,符合题意,
,符合题意,
故选D
原式各项计算得到结果,与已知结果比较即可.
此题考查了同底数幂的乘法,熟练学会运算法则是解本题的重点.
与![]() 互为倒数的是
互为倒数的是
A. ![]() B.
B. ![]() C.
C. ![]() D. 3
D. 3
【答案】A
【分析】解:![]() ,
,![]() 与
与![]() 互为倒数的是
互为倒数的是![]() .
.
故选:A.
依据乘积是1的两个数叫做互为倒数解答.
本题考查了倒数的概念,熟记定义是解题的重点.
若![]() 的积中x的二次项系数为零,则m的值是
的积中x的二次项系数为零,则m的值是
A. 1 B. ![]() C.
C. ![]() D. 2
D. 2
【答案】D
【分析】解:![]()
![]()
![]() ,
, ![]() 的积中x的二次项系数为零,
的积中x的二次项系数为零, ![]() ,
,
解得:![]() ,
,
故选:D.
先依据多项式乘以多项式法则展开,合并相同种类项,依据已知得出方程![]() ,求出即可.
,求出即可.
本题考查了多项式乘以多项式法则的应用,能正确借助法则展开是解此题的重点.
2、填空题(本大题共13小题,共32.0分)
“x与y平方的差”用代数式表示为________,“x与y差的平方”用代数式表示为________.
【答案】![]() ;
;![]() .
.
【分析】【剖析】
本题考查列代数式,要明确给出文字语言中的运算关系![]() 差的平方,先差后平方;平方的差先平方,后差
差的平方,先差后平方;平方的差先平方,后差![]() 列代数式的重点是正确理解文字语言中的关键字.
列代数式的重点是正确理解文字语言中的关键字.
【解答】
解:“x与y平方的差”用代数式表示为![]() ,
,
“x与y差的平方”用代数式表示为![]() .
.
故答案为![]() ;
;![]() .
.
长方形的周长为![]() ,宽为
,宽为![]() ,那样面积为_________.
,那样面积为_________.
【答案】![]()
【分析】【剖析】
依据长方形的周长表示出长,再依据面积公式列式计算即可得解.
【解析】
长方形的长为![]() ,
,
面积:![]() ,
,
故答案为:![]() .
.
【点睛】
本题考查了列代数式,熟练学会长方形的周长和面积公式是解题的重点.
当![]() ,
,![]() ,
,![]() 时,代数式
时,代数式![]() 的值是______ .
的值是______ .
【答案】30
【分析】解:![]() ,
,![]() ,
,![]() ,
, ![]() ,
,
故答案为:30.
将![]() ,
,![]() ,
,![]() 直接代入即可.
直接代入即可.
本题主要考查了代数式求值,直接代入是解答此题的重点.
在代数式![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() 中,单项式有______,多项式有______
中,单项式有______,多项式有______![]() 填序号
填序号![]() .
.
【答案】![]()
![]()
【分析】解:![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() 中,
中,
单项式有:![]() ,多项式有:
,多项式有:![]() .
.
故答案为:![]() ;
;![]() .
.
直接借助单项式与多项式的概念分别剖析得出答案.
此题主要考查了多项式与单项式,正确把握有关概念是解题重点.
若关于a,b单项式![]() 的系数是
的系数是![]() ,次数是5,则
,次数是5,则![]() _____,
_____,![]() _____.
_____.
【答案】![]() ,4
,4
【分析】【剖析】
此题主要考查了单项式,正确把握单项式的次数与系数确定办法是解题重点.
直接借助单项式的次数与系数确定办法剖析得出答案.
【解答】
解:![]() 是关于a,b的单项式,系数是
是关于a,b的单项式,系数是![]() ,次数是5,
,次数是5,![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,
,
故答案为![]() ,4.
,4.
把多项式![]() 按字母y的降幂排列:______.
按字母y的降幂排列:______.
【答案】![]()
【分析】解:多项式![]() 按字母y的降幂排列为:
按字母y的降幂排列为:![]()
故答案为:![]()
按字母y的指数从大到小排列即可.
此题主要考查了多项式,重点是学会降幂排列的概念.
若单项式![]() 与
与![]() 的差仍是单项式,则
的差仍是单项式,则![]() ______.
______.
【答案】![]()
【分析】【剖析】
本题考查了合并相同种类项,借助相同种类项的概念得出a、b的值是解题重点![]() 依据单项式的和是单项式,可得相同种类项,依据相同种类项的概念,可得答案.
依据单项式的和是单项式,可得相同种类项,依据相同种类项的概念,可得答案.
【解答】
解:由题意,得![]() ,
,![]() .
.
解得,![]() ,
,![]() .
.![]() .
.
故答案为![]() .
.
若一个多项式加上![]() 得到
得到![]() ,则这个多项式是________.
,则这个多项式是________.
【答案】![]()
计算:![]() __________.
__________.
【答案】![]()
【分析】【剖析】
本题考查的是同底数幂的乘法,熟悉“同底数幂的乘法是底数不变,指数相加”是解答此题的重点![]() 第一将原式变形为
第一将原式变形为![]() ,然后依据同底数幂的乘法运算法则计算即可.
,然后依据同底数幂的乘法运算法则计算即可.
【解答】
解:原式![]()
![]() .
.
故答案为![]() .
.
![]() ______.
______.
【答案】![]()
【分析】解:![]()
![]()
![]() .
.
故答案为:![]() .
.
直接借助积的乘方运算法则计算得出答案.
此题主要考查了积的乘方运算,正确将原式变形是解题重点.
如图都是由同样大小的黑棋子按肯定规律摆出的图案,第![]() 个图案有4个黑棋子,第
个图案有4个黑棋子,第![]() 个图案有9个黑棋子,第
个图案有9个黑棋子,第![]() 个图案有14个黑棋子,
个图案有14个黑棋子,![]() ,依此规律,第n个图案有1499个黑棋子,则
,依此规律,第n个图案有1499个黑棋子,则![]() ______.
______.
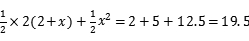 |
【答案】300
【分析】解:察看图1有![]() 个黑棋子;
个黑棋子;
图2有![]() 个黑棋子;
个黑棋子;
图3有![]() 个黑棋子;
个黑棋子;
图4有![]() 个黑棋子;
个黑棋子;![]()
图n有![]() 个黑棋子,
个黑棋子,
当![]() ,
,
解得:![]() ,
,
故答案:300
注意观察每个图形中黑棋子的个数与图形序列号的关系,找到规律,借助规律求解即可.
本题考查了图形的变化类问题,解题的重点是可以注意观察并发现图形的变化规律,困难程度不大.
![]() 的4次幂等于________________.
的4次幂等于________________.
【答案】![]()
【分析】【剖析】
本题主要考查了有理数的乘方,此题依据乘方的运算法则即可解答.
【解答】
解:![]() ,所以
,所以![]() 的四次幂等于:
的四次幂等于:![]() .
.
故答案为![]() .
.
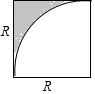 已知正方形边长为R,用含R的代数式表示右图中阴影部分的面积为______
已知正方形边长为R,用含R的代数式表示右图中阴影部分的面积为______![]() 结果保留
结果保留![]() .
.
|
【答案】![]()
【分析】解:阴影部分的面积![]() ,
,
故答案为:![]() .
.
用正方形的面积减去扇形的面积列式即可.
本题考查了列代数式,察看出阴影部分的面积表示是解题的重点.
3、计算题(本大题共3小题,共20.0分)
化简:![]()
![]() .
.
【答案】解:![]() 原式
原式![]() ;
;![]() 原式
原式![]()
【分析】![]() 原式去括号合并即可得到结果;
原式去括号合并即可得到结果;![]() 原式去括号合并即可得到结果.
原式去括号合并即可得到结果.
此题考查了整式的加减,熟练学会运算法则是解本题的重点.
化简求值:![]() 其中
其中![]() .
.
【答案】解:原式![]()
![]() ,
,
当![]() 时,
时,
原式![]()
![]() .
.
【分析】依据整式的运算法则即可求出答案.
本题考查整式的运算,解题的重点是熟练运用整式的运算法则,本题是基础题型.
数学的趣味无处不在,在学数学的过程中,小明发现了有规律的等式:![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]()
![]() 从计算过程中找出规律,可知:
从计算过程中找出规律,可知:![]() ______;
______;![]() ______
______![]() .
.![]() 计算:
计算:![]() 结果用含n的式子表示
结果用含n的式子表示![]()
![]() 对于算式:
对于算式:![]()
![]() 计算出算式的值
计算出算式的值![]() 结果用乘方表示
结果用乘方表示![]() ;
;![]() 直接写出结果的个位数字是几?
直接写出结果的个位数字是几?
【答案】![]()
![]() ;
;![]() 由
由![]() 知
知![]() ,
,
所以![]() ,
,
当![]() 时,
时,![]() ,
,
所以原式![]() .
.![]()
![]()
![]()
![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 个位数字是按3,9、7、1循环的;
个位数字是按3,9、7、1循环的;![]() ,
,
即![]() 的个位数字是第32组末位数,为1.
的个位数字是第32组末位数,为1.
【分析】解:![]() ;
;![]() .
.
故答案为:![]() ;
;![]() .
.![]() 见答案.
见答案.![]() 见答案.
见答案.![]() 依据所给出的规律可求
依据所给出的规律可求![]() ;
;![]() 依据所给出的规律可求
依据所给出的规律可求![]() .
.![]() 由规律可得
由规律可得![]() ,再把
,再把![]() 代入计算即可求解;
代入计算即可求解;![]() 变形为
变形为![]() ,再依据平方差公式即可求解;
,再依据平方差公式即可求解;![]() 先计算
先计算![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 等数字的值,找到个位数字的变化规律,进而推算出
等数字的值,找到个位数字的变化规律,进而推算出![]() 的个位数字.
的个位数字.
本题考查了平方差公式、尾数特点、整式的除法,解题的重点是注意指数的变化.
4、解答卷(本大题共5小题,共30.0分)
计算:![]() .
.
【答案】解:![]()
![]()
![]() .
.
【分析】直接借助积的乘方运算法则与同底数幂的乘法运算法则计算得出答案.
此题主要考查了积的乘方运算与同底数幂的乘法运算,正确学会运算法则是解题重点.
计算:![]() .
.
【答案】解:![]()
![]()
![]() .
.
【分析】直接借助积的乘方运算法则化简,进而合并相同种类项得出答案.
此题主要考查了幂的乘方与积的乘方运算,正确学会运算法则是解题重点.
计算:![]()
【答案】解:原式![]()
![]() .
.
【分析】直接借助单项式乘以多项式运算法则计算得出答案.
此题主要考查了单项式乘以多项式运算,正确学会运算法则是解题重点.
解方程:![]() .
.
【答案】解:原式即![]() ,
,
移项,得![]() ,
,
合并相同种类项,得![]() ,
,
系数化成1得![]() .
.
【分析】第一借助单项式与多项式,与多项式与多项式的乘法法则计算,然后移项、合并相同种类项,系数化成1即可求解.
本题考查了整式的混合运算与一元一次方程的解法,正确借助整式相乘的法则对式子进行化简是重点.
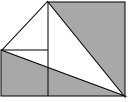 如图,将边长为2的小正方形和边长为x的大正方形放在一块.
如图,将边长为2的小正方形和边长为x的大正方形放在一块.![]() 用x表示阴影部分的面积;
用x表示阴影部分的面积;![]() 计算当
计算当![]() 时,阴影部分的面积.
时,阴影部分的面积.
【答案】解:![]() 阴影部分的面积为
阴影部分的面积为![]() ;
;![]() 时,
时,![]()
【分析】阴影部分面积借助三角形面积公式进行计算,代入已知数值即可求得面积具体数值.
此题考查列代数式问题,重点是借助三角形面积公式计算三角形的面积解答即可.







